The Power of Compounding Interest: Unlocking Financial Growth

At its core, compounding interest is a fundamental concept in the world of finance and investment. It’s often referred to as the “eighth wonder of the world” by financial enthusiasts, and for a good reason. But what exactly is it, and why does it hold such significance?

What is Compounding Interest?

Compounding interest is the process where interest is added to the principal amount of a deposit or loan, and from that moment on, the interest that has been added also earns interest. This essentially means that interest is earned on interest, leading to the exponential growth of the invested amount over time.

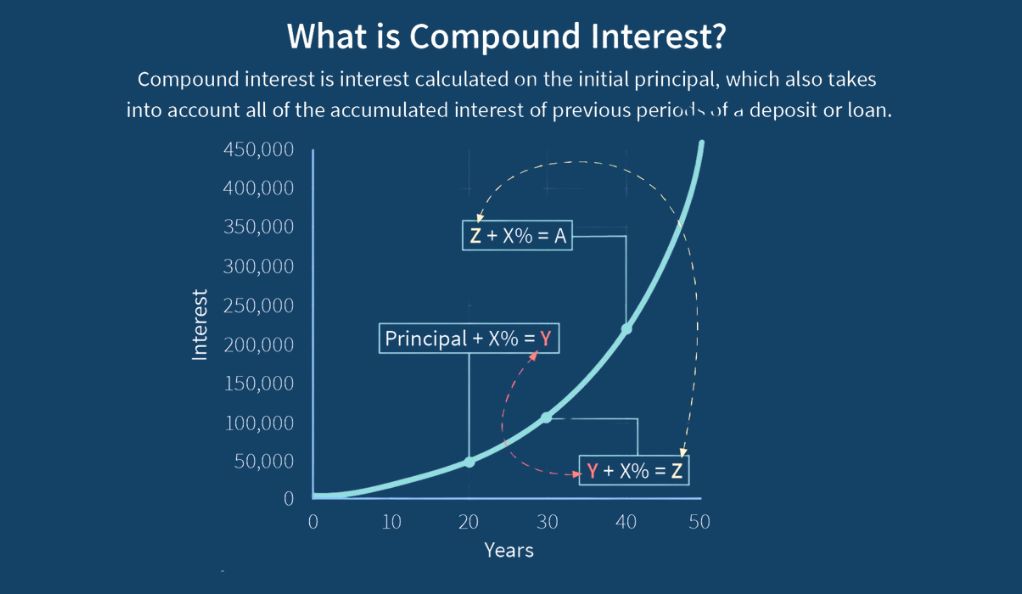
To illustrate with a simple example:

Suppose you invest $1000 at an annual interest rate of 10%. At the end of the first year, you’ll earn $100 in interest (10% of $1000). If the interest is compounded annually, in the second year, you’ll earn interest not just on your initial $1000, but also on the $100 interest from the first year. So, your interest for the second year would be $110 (10% of $1100), making your total amount $1210.

Table 1: Simple vs. Compound Interest Over 3 Years

Year	Principal (Simple)	Interest (Simple)	Total (Simple)	Principal (Compound)	Interest (Compound)	Total (Compound)
1	$1000	$100	$1100	$1000	$100	$1100
2	$1000	$100	$1200	$1100	$110	$1210
3	$1000	$100	$1300	$1210	$121	$1331

Significance in the Financial World

The power of compounding interest cannot be overstated. Here’s why it’s so revered:

1. Exponential Growth: Unlike simple interest, where the growth is linear, compounding leads to exponential growth. This means that the longer the money is invested, the faster it grows.
2. Maximizing Returns: For investors, understanding and leveraging compounding can lead to significantly higher returns over time. Even with small regular contributions, the magic of compounding can lead to substantial wealth accumulation.
3. Financial Planning: Compounding plays a crucial role in financial planning, especially when considering long-term goals like retirement. It helps individuals understand how much they need to save and invest to achieve their financial objectives.
4. Debt Implications: On the flip side, compounding can work against you when it comes to debts and loans. Credit card debts, for instance, can quickly balloon due to the compounding of interest, making it essential for consumers to understand its implications.

The Basic Principle of Compounding

Interest, in the financial realm, is the cost of borrowing money or the return earned on an investment. It’s the way lenders get compensated for the risk of lending out their money and how investors earn a return on their investments. But not all interest is created equal. There are two primary types: simple and compound. Let’s delve into their intricacies.

Simple Interest: The Straightforward Approach

Simple interest is calculated only on the principal amount, or on the portion of the principal amount which remains unpaid. It’s a linear form of growth where the interest amount remains constant year after year.

For instance, if you invest $1,000 at a simple interest rate of 5% for 2 years, your interest at the end of the two years would be:

\text{SI} = $1,000 \times 0.05 \times 2 = $100 \times 2 = $200

Compound Interest: The Power of Exponential Growth

Compound interest differs from simple interest in that it is calculated on the initial principal, which also includes all of the accumulated interest from previous periods on a deposit or loan. Think of it as “interest on interest,” and it can cause a sum to grow at a much faster rate than simple interest, which is calculated only on the principal amount.

Table 2: Simple vs. Compound Interest Over 5 Years on a $1,000 Investment at 5% Annual Rate

Year	Total with Simple Interest	Total with Compound Interest (Annually Compounded)
1	$1,050	$1,050
2	$1,100	$1,102.50
3	$1,150	$1,157.63
4	$1,200	$1,215.51
5	$1,250	$1,276.28

Math Behind Compounding

The reason compound interest leads to faster growth than simple interest is due to the reinvestment of interest. With simple interest, you earn interest only on the principal. With compound interest, in each period, interest is calculated on the sum of the principal and the accumulated interest from previous periods.

For instance, in the table above, by the end of the second year, the compound interest calculation earns interest on the initial $1,000 and the $50 interest from the first year, leading to a total of $1,102.50. This compounding effect becomes more pronounced over longer periods, leading to an exponential growth curve.

Historical Context

The concept of interest, and by extension, compounding interest, is not a modern invention. Its roots can be traced back thousands of years, intertwined with the history of trade, commerce, and the evolution of financial systems.

Origins of Compounding Interest

The earliest recorded use of interest dates back to ancient civilizations. The Sumerians, who lived in Mesopotamia (modern-day Iraq) around 2000 BC, are credited with the first known use of interest. They used it in the context of agricultural loans, where farmers borrowed seeds and repaid with a portion of their harvest, effectively paying “interest” on the borrowed seeds.

However, the concept of compounding interest specifically took a bit longer to develop. Ancient texts from India, dating around 600 BC, hint at a deeper understanding of the mathematics of compound interest. The Arthashastra, an ancient Indian treatise on statecraft and economic policy, mentions concepts that resemble compound interest.

Famous Figures and Their Exploits with Compounding

1. Richard de Witney (13th Century): One of the earliest recorded uses of compound interest in Europe was by Richard de Witney in 1275. He lent money to the English Crown and was allowed to compound the interest, which was a novel concept in Europe at the time.
2. Benjamin Franklin (18th Century): The famous American polymath is often associated with the adage, “A penny saved is a penny earned.” But Franklin’s appreciation for compounding went beyond mere sayings. In his will, he left 1,000 pounds each to the cities of Boston and Philadelphia, stipulating that the money should be invested and compounded for 200 years. By the end of the period, the funds had grown exponentially, showcasing the power of compound interest over long durations.
3. Warren Buffett (20th-21st Century): Often hailed as one of the greatest investors of all time, Buffett’s investment strategy heavily relies on the power of compounding. His long-term investment approach, combined with the consistent returns he achieves, has allowed his wealth to grow exponentially over the decades. Buffett often emphasizes the importance of patience in investing, allowing compounding to work its magic over time.

The Evolution and Impact of Compounding

As civilizations evolved and financial systems became more sophisticated, the understanding and application of compounding interest grew. By the Renaissance period, European merchants and bankers had fully embraced the concept, using it in various financial instruments and contracts.

The power of compounding interest has not only shaped the fortunes of individuals but has also played a pivotal role in the economic development of nations. It has influenced lending and borrowing policies, banking systems, and investment strategies, leaving an indelible mark on the world of finance.

Real-world Examples

To truly grasp the transformative power of compounding interest, it’s beneficial to see it in action through real-world examples. These scenarios, grounded in everyday experiences, can illuminate how compounding can significantly amplify wealth over time.

Scenario 1: The Retirement Savings

Imagine two friends, Alice and Bob. Both decide to save for retirement, but they start at different ages:

• Alice starts saving $200 every month at age 25 and stops at age 35, investing for 10 years. Her investment earns an annual compound interest rate of 7%.
• Bob starts saving $200 every month at age 35 and continues until age 65, investing for 30 years with the same 7% annual compound interest rate.

By the time both reach 65, who will have more money?

Surprisingly, even though Alice only invested for 10 years compared to Bob’s 30 years, due to the power of compounding, Alice will have a larger amount at 65.

Table 1: Alice vs. Bob’s Retirement Savings

Individual	Total Contributions	Total Amount at Age 65
Alice	$24,000	$602,070
Bob	$72,000	$303,219

Scenario 2: The College Fund

A couple decides to start a college fund for their newborn child. They invest an initial amount of $5,000 and add $100 every month. With an annual compound interest rate of 5%, by the time the child turns 18, the fund will have grown substantially.

Using the compound interest formula, the total amount after 18 years would be approximately $41,095. This showcases how regular contributions, combined with compounding, can lead to significant growth over time.

The High School Student’s Investment Journey

Drawing from the Penn article, let’s delve into the story of a high school student, Jamil. After working summers at a cupcake shop, Jamil accumulated some savings. Recognizing that leaving his earnings in a simple savings account might erode his purchasing power due to inflation, he embarked on an investment journey.

Jamil’s steps:

1. Research: He began by reading articles on Investopedia, trying to understand the basics of investing in stocks and bonds.
2. Passive Investments: Realizing he didn’t want to actively manage his investments, Jamil turned to passive investments like mutual funds.
3. Opening a Brokerage Account: After understanding mutual funds, he opened a brokerage account with TD Ameritrade, investing in a well-diversified mutual fund.
4. Understanding Compound Interest: Over time, Jamil recognized the power of compound interest. He realized that not only was he earning returns on his principal amount but also on the interest that kept accumulating.

For instance, if Jamil invested $1,000 with an 8% return, by the end of the year, he’d have $1,080. With compound interest, if he reinvested the $1,080 the next year, he’d end up with $1,166.40 by the end of the second year. This is in contrast to simple interest, which would’ve given him $1,160.

Jamil’s journey underscores the importance of starting early and allowing compound interest to work over time. It also highlights the significance of financial literacy and making informed decisions.

The Magic of Time and Consistency

In the realm of finance and investment, time is often considered the most potent factor. Its significance is amplified when combined with the power of compounding interest. The interplay between time, consistency, and compounding can lead to astonishing financial outcomes.

The Importance of Starting Early

1. The Snowball Effect: Just as a snowball grows larger as it rolls down a hill, the effect of compounding interest accumulates more significantly over time. The earlier you start investing, the more time your money has to grow and benefit from this effect.
2. The Power of Additional Compounding Periods: Starting early means more compounding periods for your investment. Even if the difference is just a few years, it can lead to a substantial difference in the end amount due to the exponential nature of compounding.
3. Mitigating Market Volatility: Starting early also provides a longer horizon to ride out the ups and downs of the market, allowing investors to benefit from potential higher returns in the long run.

Table 1: Impact of Starting Age on Final Investment Value

Starting Age	Monthly Contribution	Annual Return	Value at Age 65
25	$200	7%	$525,479
30	$200	7%	$362,688
35	$200	7%	$246,725
40	$200	7%	$165,489

Note: The above table assumes consistent monthly contributions until age 65.

Exponential Growth Over Long Periods

1. Understanding Exponential Growth: Unlike linear growth, where the increase is constant, exponential growth means the investment grows at a rate proportional to its current value. In the context of compounding, it means the interest earned is continually reinvested, leading to interest on interest.
2. The Rule of 72: A quick way to estimate how long it will take for an investment to double at a fixed annual rate of compound interest is the Rule of 72. You simply divide 72 by the annual rate of return. For instance, at a 6% return, it would take approximately 12 years (72 ÷ 6) for the investment to double.
3. Consistency is Key: While the rate of return is essential, consistency in contributions can also lead to significant growth over time. Regular contributions, even if they’re small, can accumulate and compound to substantial sums over extended periods.

Graphical Representation: Growth of $10,000 Over Different Time Spans

Imagine an initial investment of $10,000 with an annual compound interest rate of 5%. Over different time spans, the growth would look something like this:

• 10 years: $16,386
• 20 years: $26,532
• 30 years: $43,219
• 40 years: $70,400

This progression showcases the exponential nature of growth, especially as the time span increases.

Compounding in Different Investment Vehicles

Compounding isn’t exclusive to any single type of investment. Its principles apply across various investment vehicles, from stocks to bonds and beyond. However, the nature, risk, and return of each vehicle can influence how compounding manifests.

Stocks

• Nature: Stocks represent ownership in a company. When you buy a stock, you own a piece of that company and stand to gain (or lose) based on its performance.
• Compounding Aspect: Stocks don’t compound in the traditional sense of earning interest on interest. Instead, their compounding effect comes from reinvesting dividends or capital gains. If a stock pays dividends, reinvesting those dividends to buy more shares can lead to a compounding effect over time.

Bonds

• Nature: Bonds are debt securities. When you buy a bond, you’re essentially lending money to the issuer (like a government or corporation) in exchange for periodic interest payments and the return of the bond’s face value when it matures.
• Compounding Aspect: Bonds typically pay interest semi-annually. If this interest is reinvested, it can earn more interest, leading to a compounding effect. The frequency of interest payments and the reinvestment of those payments play a crucial role in how bonds compound.

Mutual Funds

• Nature: Mutual funds pool money from multiple investors to invest in a diversified portfolio of stocks, bonds, or other securities.
• Compounding Aspect: Mutual funds can compound in several ways. Dividends or interest earned by the fund’s holdings can be reinvested to buy more shares of the fund. Additionally, if the fund’s assets appreciate, the value of each share of the fund increases, leading to capital gains. Reinvesting these gains can further amplify the compounding effect.

Certificates of Deposit (CDs)

• Nature: CDs are time deposits offered by banks with a fixed term. They typically offer higher interest rates than regular savings accounts.
• Compounding Aspect: Interest on CDs can be compounded at different intervals, such as daily, monthly, or annually. The frequency of compounding can significantly affect the total interest earned by the end of the CD’s term.

Table 1: Impact of Compounding Intervals on a 1-Year $10,000 CD at 3% Annual Rate

Compounding Interval	Total Interest Earned	End Balance
Daily	$304.04	$10,304.04
Monthly	$303.60	$10,303.60
Annually	$300.00	$10,300.00

How Different Rates and Intervals Affect Compounding

1. Rates: The rate of return or interest rate is a primary driver of compounding. A higher rate means more interest or returns earned, which when reinvested, leads to faster compounding. Even a small difference in rates can lead to significant differences in end balances over long periods.
2. Intervals: The frequency of compounding can also play a significant role. The more frequent the compounding, the more opportunities there are for earnings to be reinvested and earn more returns. For instance, daily compounding will lead to faster growth than annual compounding, given the same rate.

Strategies to Maximize Compounding Benefits

While the principle of compounding is straightforward, maximizing its benefits requires strategic planning and disciplined execution. Here, we’ll explore actionable strategies that investors can employ to harness the full power of compounding.

1. Start Early and Stay Consistent

• The Advantage of Time: As previously discussed, time is a crucial factor in compounding. The longer your investments have to compound, the more significant the benefits. Even if you start with a small amount, beginning early can lead to substantial growth over time.
• Consistent Contributions: Regularly adding to your investments, whether monthly, quarterly, or annually, can amplify the compounding effect. These consistent contributions, combined with the returns they generate, can lead to exponential growth over time.

2. Reinvest Dividends and Interest

• Harnessing Additional Growth: When you earn dividends from stocks or interest from bonds or savings accounts, reinvesting these earnings can supercharge the compounding effect. Instead of taking these payouts as cash, use them to buy more shares or units of the investment.
• The Snowball Effect: Think of reinvesting dividends and interest as adding more snow to a snowball. The more you add, the bigger it gets, and the faster it grows as it rolls down the hill.

3. Minimize Withdrawals

• Letting Compounding Work: Every time you withdraw from your investments, you reduce the principal amount that’s working for you. Minimizing or delaying withdrawals allows the compounding engine to run at its full capacity.

4. Diversify Investments

• Spread and Compound: Diversifying across different investment vehicles (stocks, bonds, mutual funds, etc.) can provide multiple avenues for compounding. Different assets have varying rates and intervals of returns, and a diversified portfolio can harness the benefits of each.

5. Monitor and Adjust

• Stay Informed: Regularly review your investments to ensure they’re performing as expected. If certain assets aren’t providing satisfactory returns, consider reallocating to better-performing ones.
• Adapt to Life Changes: As you progress through different life stages, your financial goals and risk tolerance may change. Adjust your investment strategy accordingly to maximize compounding benefits aligned with your goals.

Table 1: Growth of a $10,000 Investment Over 20 Years at 7% Annual Return

Strategy	End Balance
No reinvestment of dividends/interest	$38,696.84
Reinvestment of dividends/interest	$42,047.78
Regular monthly contributions of $100	$98,358.24
Combination of all strategies	$101,709.18

The Power of Reinvesting

Reinvesting dividends and interest is a cornerstone strategy for maximizing compounding benefits. By continually adding to the principal amount, you’re not just earning returns on your initial investment but also on the returns themselves. Over extended periods, this can lead to growth curves that are steeper and more pronounced than those of investments where returns are not reinvested.

The Dark Side: Compounding Debt

While compounding can be an investor’s best friend, it can also be a formidable foe when it comes to debt. Just as compounding can amplify wealth over time, it can also magnify debt, especially when it’s not managed prudently.

Understanding Compounding in the Context of Debt

1. Credit Card Debt: One of the most common arenas where compounding can work against consumers is credit card debt. Credit cards often have high-interest rates, and when balances aren’t paid in full, the remaining amount is subject to interest. This interest is then added to the principal, and the next month, interest is charged on this new, larger amount. This cycle can lead to rapidly ballooning debt.
2. Loans: Whether it’s a personal loan, mortgage, or student loan, if they compound, the principles are similar. Interest accrues on the principal, and if it’s not paid off, the interest can compound, leading to larger and larger debt amounts.

Table 1: Growth of a $5,000 Credit Card Debt at 18% Annual Interest

Year	Balance Without Payment	Balance with Minimum Payment ($150/month)
1	$5,900	$5,410
2	$6,962	$5,884
3	$8,215	$6,424
4	$9,694	$7,040
5	$11,439	$7,737

Note: This table assumes no additional charges on the card.

Strategies to Mitigate the Negative Impact of Compounding Debt

1. Pay More Than the Minimum: Especially with credit cards, paying only the minimum due can lead to significant interest charges. Always aim to pay more than the minimum, or better yet, pay off the full balance each month.
2. Refinance or Consolidate: If you have high-interest loans or multiple debts, consider refinancing to a lower interest rate or consolidating your debts. This can reduce the amount of interest that compounds over time.
3. Avoid Unnecessary Debt: It might sound obvious, but the best way to avoid the negative effects of compounding debt is not to accumulate it in the first place. Be cautious with credit card spending, and avoid taking on high-interest loans unless absolutely necessary.
4. Set Up Automatic Payments: By automating your debt payments, you ensure that you never miss a due date. Late payments can lead to additional fees and higher interest rates, exacerbating the compounding effect.
5. Educate Yourself: Understand the terms of your loans and credit cards. Know the interest rates, how often interest compounds, and any fees associated with the debt.
6. Seek Professional Advice: If you find yourself overwhelmed by compounding debt, consider seeking advice from a financial counselor or advisor. They can provide strategies tailored to your situation.

Conclusion

In the intricate tapestry of finance, few concepts hold as much transformative power as compounding. Often dubbed the ‘eighth wonder of the world,’ its ability to amplify wealth over time has been the cornerstone of many investment strategies and the foundation of countless fortunes. From its historical roots in ancient civilizations to its modern-day applications in diverse investment vehicles, compounding’s influence is pervasive.

However, like a double-edged sword, compounding’s effects aren’t solely beneficial. When applied to debt, especially in the realms of high-interest credit cards and loans, it can quickly turn from a boon to a bane, amplifying financial burdens just as effectively as it can wealth.

Yet, with knowledge, strategy, and discipline, individuals can harness the positive aspects of compounding while mitigating its pitfalls. Whether you’re an investor looking to maximize returns or a consumer navigating the complexities of debt, understanding and respecting the power of compounding is paramount. In the dance of numbers that is finance, compounding leads, and those who master its steps are poised for success.